День добрый, дорогой друг!
Спасибо, что заходите на наш телеграм канал и пишете комментарии к статьям.
В предыдущей статье мы с вами разбирали коэффициент Бухгольца. Что это за штука, когда и где он применяется. Сегодня под нашим пристальным взором коэффициент Бергера, — в своем роде «сводный брат» Бухгольца.
Содержание статьи
Что это такое?
Коэффициент Бергера представляет собой дополнительный числовой показатель и используется для ранжирования участников в турнирной таблице. Принимается во внимание только в случае равенства очков участников.
Автором идеи является чех Оскар Гельбфус, предложивший подобный способ ранжирования в 1873г. В турнирную практику коэффициент Бергера вошел начиная с турнира в Ливерпуле в 1882 году благодаря усилиям Уильяма Зоннеборна и Иоганна Бергера.
Как видите, история распределения мест с помощью «Бергера» прошла более чем солидную проверку временем.
Коэффициент Бергера применяется в турнирах по круговой системе. Когда все участники играют между собой по очереди.
Как считать?
Спешу вас успокоить, никакой высшей математики здесь нет. При желании можно посчитать все в уме.
Формула для посчета коэффициента Бергера выглядит следующим образом:
КБ = СуммаВ + 1/2 суммыН, где
СуммаВ — Сумма очков соперников у которых участник выиграл
СуммаН — Сумма очков соперников, с которыми участник сыграл вничью.
Очки соперников, которым участник проиграл, — не учитывается. Вернее сумма считается равной нулю.
Например:
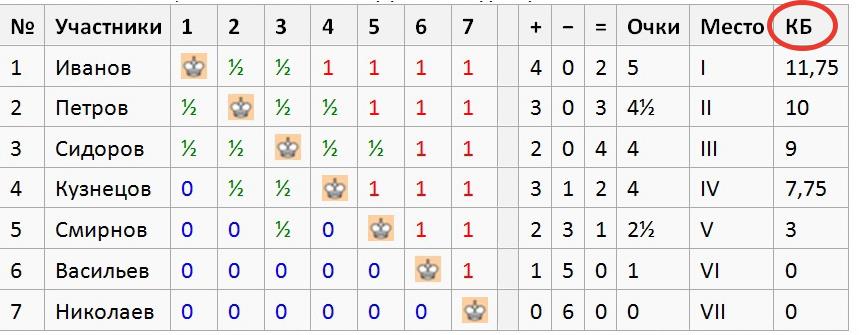
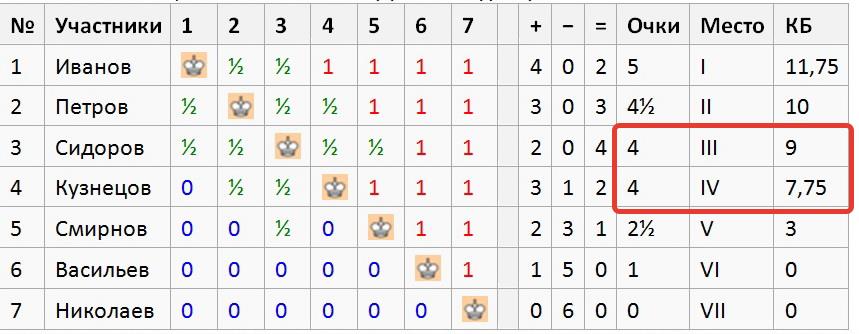
В таблице, приведенной выше, Сидоров и Кузнецов набрали по 4 очка. Для ранжирования в иоговой таблице турнира посчитаем «Бергер» этих участников:
Сидоров: 1 + ½* (5 +4.5 +4 +2.5) = 9
Кузнецов: (2.5 +1) + ½* (4.5 +4) = 7.75
Таким образом, Сидоров опережает Кузнецова в турнирной таблице при равенстве очков по дополнительному показателю – коэффициенту Бергера.
Логика «Бергера»
Небольшое отступление: Если Вы или ваш ребенок делаете только первые шаги в шахматах, – профессионально проконсультируем и подберем программу обучения, подходящую именно вам
Любой дополнительный показатель, влияющий на итоговое распределение мест в таблице должен иметь определенную логику. Как бы нести в себе «зерно справедливости».
Логика «Бергера» определяется формулой расчета коэффициента: преимущество имеет игрок, набирающий больше очков против более сильных соперников.
Не скажу, что такая логика безоговорочно справедлива и не может вызывать вопросов.
Возможно поэтому, в последние годы для определения призовых мест, часто вместо дополнительных показателей практикуются дополнительные партии с укороченным контролем. Что не говори, результат за доской всегда в приоритете.
Однако и без дополнительных показателей, особенно при распределении не призовых мест, вряд ли можно обойтись. В почти полутора-вековой истории шахмат ничего более адекватного, чем КБ никто не придумал.

Коэффициент Бергера по-прежнему живет и здравствует также как в 1882г. в Ливерпуле.
Упрощенный подсчет
Примерно с восьмидесятых годов вошел в практику и упрощенный подсчет.
Считается еще проще: Очки поверженных соперников плюсуются, очки тех, кому уступил, — минусуются (берутся со знаком минус). Сумма считается простым арифметическим сложением.
Такой способ упрощает расчеты.
Типичная ошибка
Для турнирной борьбы обычной является такая ситуация: перед последним туром участники прикидывают коэффициенты. Для того, чтобы выбрать тактику на последнюю партию. Например, шахматист Петров думает:
«Мне достаточно сделать ничью, ибо если Иванов обыграет Пупкина и догонит меня по очкам, Бергер у меня лучше»
И Петров соглашается на ничью в позиции с отличными шансами на победу, предвкушая процедуру награждения.
Однако при подсчете коэффициентов вдруг оказывается, что его Бергер хуже, чем у Иванова!

Секрет прост. В последнем туре игрались партии и начислялись очки. Петров же при своих прикидках ориентировался на «очковую массу», которая была актуальна до последнего тура.
Хорошо, когда вы играете в команде, есть тренер или другой человек, который «считает» все эти нюансы. Часто в режиме «онлайн» по ходу последнего тура. Также не составляет труда сделать какой-нибудь калькулятор.
Однако отвлекаться на подобные вещи во время партии весьма рискованно. Полагаю, излишне объяснять, что лучшая математика – победа за доской.
Благодарю за интерес к статье.
Если вы нашли ее полезной, сделайте следующее:
- Поделитесь с друзьями, нажав на кнопки социальных сетей.
- Напишите комментарий (внизу страницы)
- Подпишитесь на обновления блога (форма под кнопками соцсетей) и получайте статьи к себе на почту.

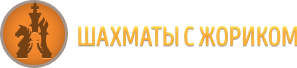



Почему в приведенном примере очки тех игроков, с которыми наши герои сыграли в ничью взяты в уполовиненом виде, а потом ещё раз уполовинены?
Это ошибка. Исправлено, спасибо
А как быть с + и — (плюсами и минусами)
Игрок получил очко без игры за неявку соперника.
При подсчете коэф. бергера оно учитывается как обычное очко?
Нет, в этом случае в коэффициенте будет засчитано 0 !